Calculating the Moment of Inertia
AdeptSix 300CR Robot Instruction Handbook, Rev. A 59
Example 3
The following example shows how to calculate the center of gravity in cases where more
then two workpieces, such as the dual end effector system shown in Figure 5-8, are
utilized.
1. Define the center of gravity, based on the position of the center of gravity of the
tool being used, and define the moment of inertia based on the center of gravity of
the entire tool. Use the hexahedron and cylinder principle as described in
“Example 1” on page 54.
2. When the weight of each part and the center of gravity have been defined, the
position of the center of gravity, including the moment of inertia at the center of
gravity, can be calculated for the entire tool. Refer to “Example 1” on page 54 and
“Example 2” on page 57 for details.
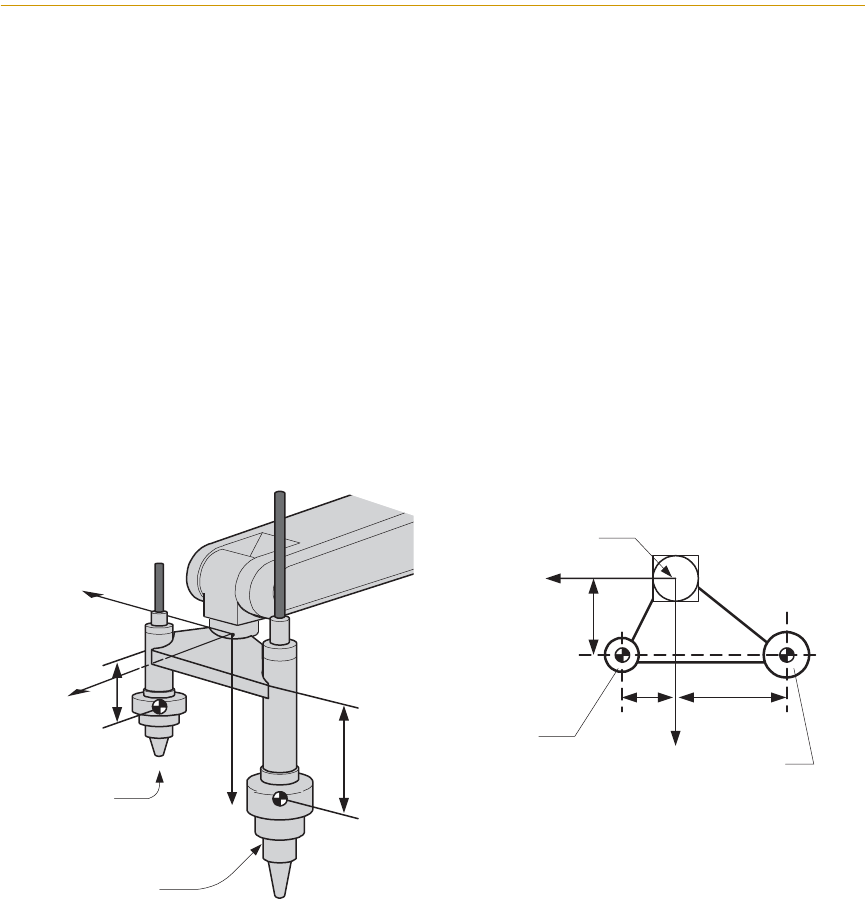
Figure 5-8 shows how to calculate the required values.
Figure 5-8. Center of Gravity: Dual End Effector Example
Weight: W=w1+w2 = 3+6 = 9. Approx. 10 kg
Center of gravity: g=(w1*x1+w2*x2)/(w1+w2)
= (3*100+6*100)/(3+6) = 100 mm
Yg= (3*50+6*(-150))/(3+6) = -83.333 mm
Zg= (3*40+6*70)/(3+6) = 60 mm
The moment of inertia at the center of gravity:
lx = {w1*((y1-Yg)²+(z1-Zg)²)*10
-6
+lcx1}
+ {w2*((y2-Yg)²+(z2-Zg)²)*10
-6
+lcx2}
= 3*((50(-83))² + (40-60)²* 10
-6
+ 6*(((-150) – (-83))²+(70-60)²)* 10
-6
= 0.082 = Approx. 0.100
ly = 3*((100-100)²+(40-60)²)* 10
-6
+ 6*((100-100)²+(70-60)²)* 10
-6
F
X
Z
Y
X
Y
40
70
Gun 1
Gun 2
F
F
(Gun 1)
Weight: w1 = 3 kg
Center of Gravity:
x1 = 100 mm
y1 = 50 mm
z1 = 40 mm
(Gun 2)
Weight: w2 = 6 kg
Center of Gravity:
x2 = 100 mm
y2 = -150 mm
z2 = 70 mm
F
F
Center of Flange
100
50 150
Gun 1
Gun 2
(Top View)
