Parker Hannifin
Chapter 5 Tuning 81
commanded position. Under these circumstances, a position error will
accumulate no matter how high the gains are set.
Servo Response Overview
Stability
The first objective of tuning is to stabilize the system. The formal definition of
system stability is when a bounded input is introduced to the system, the
output of the system is also bounded. What this means to a motion control
system is if the system is stable, and the position setpoint is a finite value,
the final actual position of the system is also a finite value.
In contrast, if the system is unstable, no matter how small the position
setpoint or how little a disturbance (motor torque variation, load change,
noise from the feedback device, etc.) the system receives, the position error
will increase exponentially in almost all cases. In practice, when the system
experiences instability, the actual position will oscillate in an exponentially
diverging fashion as shown in Table 38.
One commo
n misperception is that whenever there is oscillation, the system
is unstable. It is important to recognize that a system is considered stable if
the oscillation finally diminishes (damps out), even if it takes a long time.
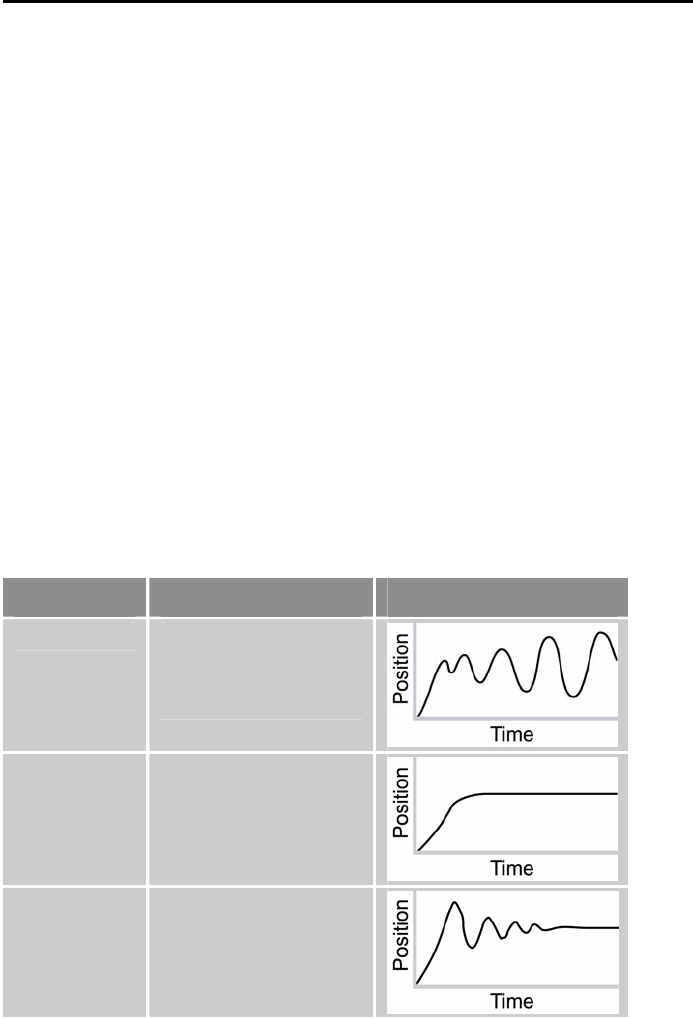
Position Response Types
Table 38 identifies the six basic types of position responses. The primary
difference among these responses is due to damping—the suppression (or
cancellation) of oscillation.
Response Description Profile (position/time)
Unstable
Instability causes the
position to oscillate in
an exponentially
diverging fashion.
Over-
damped
A highly damped, or
over-damped, system
gives a smooth but
slower response.
Under-
damped
A slightly damped, or
under-damped,
system gives a slightly
oscillatory response.


















