© National Instruments Corporation 5-1 Xmath Control Design Module
5
Classical Feedback Analysis
The open-loop systems analyzed in Chapter 4, System Analysis, generally
perform in a satisfactory manner only if the system model is very accurate
and there are no external disturbances. These conditions usually are not
met. Feedback presents an effective way to control the output of a system.
The functions in this chapter address the problem of suitably controlling
an open-loop plant through output feedback. They are most often applied
to single-input, single-output (SISO) systems. With the exception of
rlocus( )
and bode( ), these functions also can be used with
multi-input, multi-output (MIMO) systems.
Feedback Control of a Plant Model
The key principle of feedback is that the output of a system be fed back,
compared to a reference or “desired” output value, and then the error
between the two terms used to correct the system’s output so that it matches
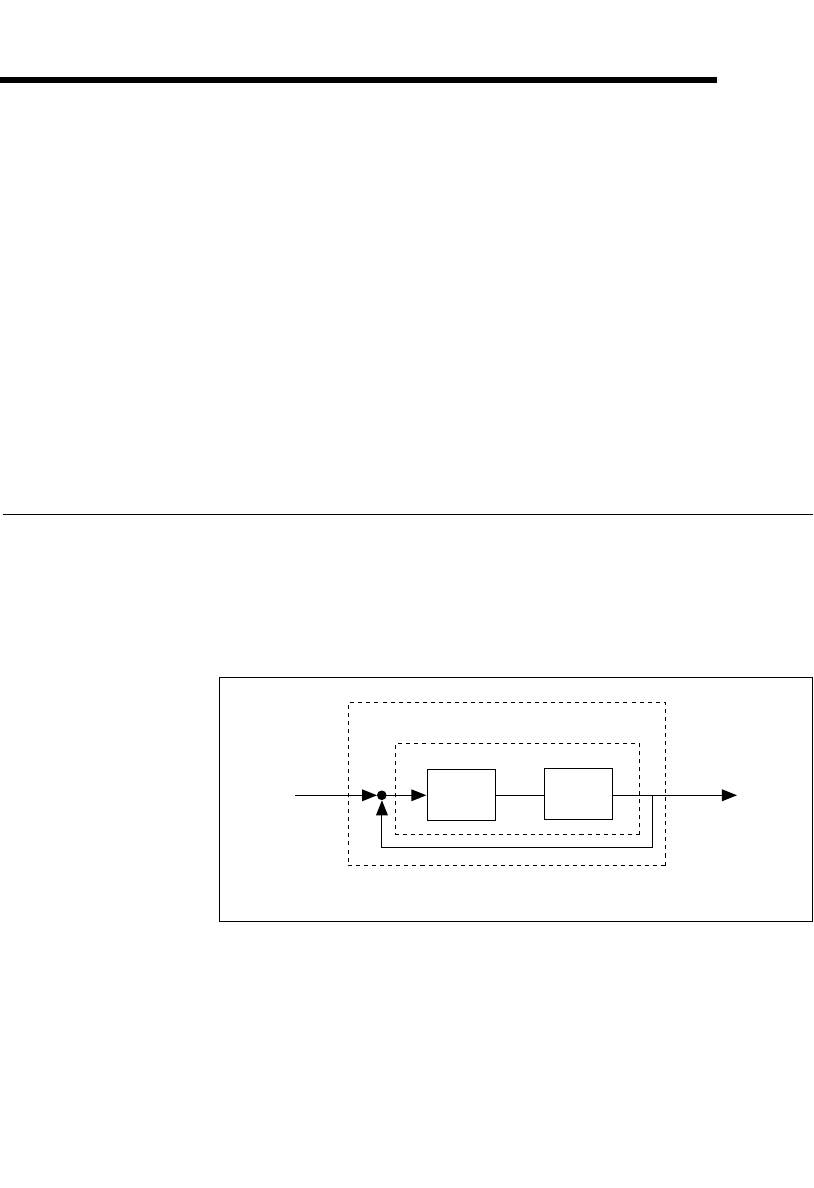
the reference. The basic diagram of a feedback control system is shown in
Figure 5-1.
Figure 5-1. Feedback Control System Block Diagram
The output of the open-loop system is KH(s); the output of the closed-loop
system shown in Figure 5-1 is given by:
U(s) Y(s)R(s)
K
+
–
H(s)
G(s)
G
cl
(s)
Ys()
Rs()
-----------
KH s()
1 KH s()+
-------------------------=


















