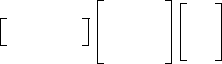
Chapter 6 State-Space Design
© National Instruments Corporation 6-13 Xmath Control Design Module
For continuous-time systems,
the quadratic performance index takes the form:
For the discrete case where the system is defined as a multistage process:
the performance index is defined similarly except that a summation sign
replaces the integral of the preceding quadratic performance index
equation.
R
xx
is a real, symmetric, positive-semidefinite matrix indicating the
weighting of the cost on the elements of the state vector x. R
uu
is a real,
symmetric, positive-definite matrix indicating the weighting of the cost on
the control inputs given by the vector u. R
xu
is a real matrix indicating the
cross-weighting of the cost between states and inputs; for many
applications, it will consist of all zeros if the control and states are
uncorrelated.
Bryson and Ho showed in [BH75] that the optimal control which
minimized this quadratic performance index is a linear feedback
combination of the states, u = K
r
x, for both the continuous and discrete
cases.
For the continuous case, K
r
is defined as follows, with P solving the
continuous-time Riccati equation:
and for the discrete case, P solves the discrete Riccati equation.
x
·
Ax Bu+=
J
x' t()u' t()
R
xx
R
xu
R
xu'
R
uu
xt()
ut()
dt
0
∞
∫
=
x
k 1+
Ax
k
Bu
k
+=
K
r
R
uu
1–
B'PR
xu
+()=
R
xx
PA A′PPBR
xu
+()R
uu
1–
R
xu′
B′P+()–++ 0=
A'PA A'PB R
xu
+()R
uu
B'PB+()
1–
B'PA R′
xu
+()– R
xx
+ P=
K
r
R
uu
B'PB+()
1–
B'PA R
xu
+()=


















