Chapter 1 Introduction
© National Instruments Corporation 1-13 Xmath Control Design Module
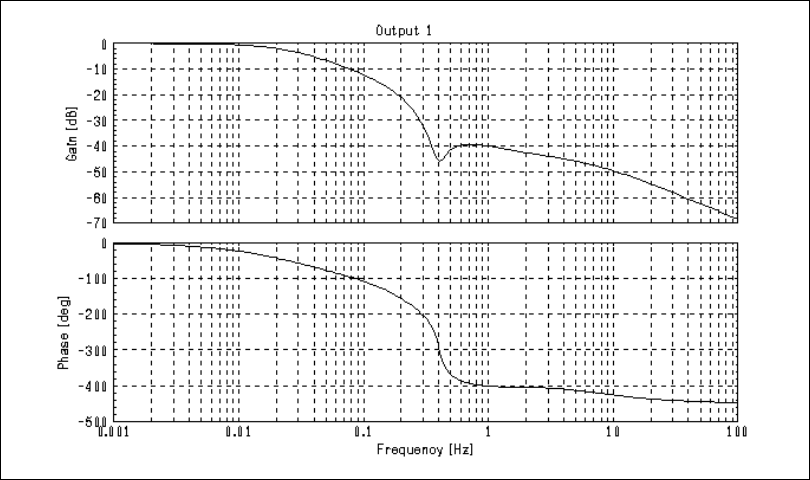
Figure 1-6. Closed-Loop System Bode Plot
The domain of the gain and phase margin PDMs indicates the frequency
(in hertz) at which the margin occurs. So the gain can be increased by about
26.1 dB before the system becomes unstable.
Helicopter Hover Problem: State Feedback and Observer Design
The approach taken in the Helicopter Hover Problem: An Ad Hoc
Approach section, although producing a desirable response, often cannot
be used in practice because uncertainty in modeling generally precludes
exact knowledge of the location of the pole one plans to cancel.
Another approach is to feed the information obtained from the states back
to the inputs through gains calculated to relocate the closed-loop poles.
Refer to the Controllability section of Chapter 6, State-Space Design,
for more information. For this approach, you first need to verify that your
system is controllable and observable. When you have confirmed that it
is—that there are no hidden modes—you can design a full-state feedback
control law that will place the system eigenvalues at values that will yield
a stable system. Because the system is observable, you then can design an
estimator to yield estimates for the missing states. Again, you will require
that your system track a step input.


















